When listening to music, we are often drawn to the main melody or rhythm of a song. However, what we may not realize is that there are other sounds present in the music that contribute to its overall quality.
These sounds are known as overtones and fundamentals. Fundamentals are the main or primary sounds that we hear in music. They are the notes that make up the melody and chords of a song.
Overtones, on the other hand, are additional sounds that are produced when a note is played. These sounds are not as prominent as the fundamentals but they play a crucial role in the overall sound of the music.
Overtones have a harmonic relationship with the fundamentals, meaning they are related to them in a mathematical way. This relationship is what gives music its unique sound and character.
For example, when a guitar is played, the fundamental note is the sound of the string vibrating at its base frequency. However, there are also overtones present that are produced by the string vibrating at multiples of its base frequency.
These overtones give the guitar its distinct sound. In music production, overtones can be manipulated to create new sounds and textures. By emphasizing certain overtones and filtering out others, producers can create a unique sound that sets their music apart from others.
This is often done in genres such as electronic music where producers use synthesizers to create new and unique sounds. In conclusion, while fundamentals are the main sound we hear in music, overtones play a crucial role in creating the overall sound and character of a song.
They are often overlooked but can be manipulated to create new and unique sounds in music production. Understanding the relationship between overtones and fundamentals can help us appreciate and enjoy music on a deeper level.
Table of Contents
All About Overtones
Overtones, also known as partials or harmonics, are additional frequency components that coexist with the fundamental frequency of a sound.
When a complex sound is analyzed in the frequency domain (using Fourier analysis, for example), it can be represented as a sum of sine waves at different frequencies, each with its own amplitude and phase.
The lowest frequency sine wave is the fundamental frequency, which corresponds to the perceived pitch of the sound. The higher-frequency sine waves are the overtones, and their amplitudes and phases contribute to the timbral characteristics of the sound.
In mathematical terms, if the fundamental frequency is denoted as “f0,” the nth overtone has a frequency of n * f0, where “n” is a positive integer greater than or equal to 2.
The strength and distribution of these overtones determine the unique timbre of a sound source, such as a musical instrument or a human voice.
Let’s say you play the same, not A2, on two different instruments: a guitar and a piano. At the core, the frequency that plays in both instruments is 110 Hz (A2). However, what differentiates the timbre (the unique identifying tone of the instrument) of both instruments are the overtones or the additional frequencies that support the fundamental frequency.
Timbre (or the overtones structure of an instrument) is what makes any two instruments or voices different.
Harmonics, specifically, refers to the overtones that are integer multiples of the fundamental frequency. The first harmonic is equivalent to the fundamental frequency itself (n = 1), the second harmonic is twice the fundamental frequency (n = 2), the third harmonic is three times the fundamental frequency (n = 3), and so on.
All About Fundamentals
The fundamental frequency is a complex sound’s lowest and primary frequency that defines its pitch. When you hear a musical note or any sound, the fundamental frequency is the primary tone that you perceive, and it gives the note its fundamental pitch.
In music, fundamental frequencies are essential because they determine the note’s position on the musical scale. The fundamental frequency is directly related to the perceived pitch of the sound, and it is the frequency used to name musical notes.
For any two instruments or voices playing the same note yet sounding different, the common link is the fundamental frequency they are playing. The fundamental frequencies of the various musical notes in equal temperament tuning are as follows:
- A4 (A above middle C) – 440 Hz
- B4 – 493.88 Hz
- C5 – 523.25 Hz and so on…
The frequencies above continue to double or halve as we move up or down the musical scale. For example, the A3 note below A4 will have a fundamental frequency of 220 Hz, and the A5 note above A4 will have a fundamental frequency of 880 Hz.
Fundamental frequencies are significant in various aspects of audio engineering and music production. They are used in sound synthesis to generate pure tones and build more complex waveforms with harmonic content.
In sound processing, equalization (EQ) is often used to boost or attenuate specific frequencies, including the fundamental frequencies, to shape the timbre of the sound.
Overtones vs Fundamentals in Music
In music, the concepts of overtones and fundamentals are fundamental to understanding the timbre or tone colour of musical notes and instruments. Let’s explore the key differences between overtones and fundamentals.
But before that, let’s look at both through the lens of Sine Wave. In a perfect sine wave, there are no overtones. A sine wave represents a single frequency with no additional frequencies present.
It is the purest form of a sound, containing only the fundamental frequency. It has a smooth, regular waveform. However, when the sine wave undergoes distortion, either intentionally or unintentionally, the shape of the waveform is altered, and harmonics are introduced.
These harmonics are overtones at frequencies that are integer multiples of the original fundamental frequency. The combination of the fundamental frequency and these overtones gives the distorted waveform its complex and rich sound.
In musical contexts, intentional distortion (e.g., in guitar amplifiers) is often used to add character and warmth to the sound by introducing desirable overtones.
Fundamental Frequencies
The fundamental frequency is the lowest and primary frequency of a musical note or sound. It is the frequency that determines the perceived pitch of the sound.
When you play a single note on a musical instrument, the fundamental frequency is the primary tone you hear. It is what allows you to distinguish between high and low-pitched notes.
In musical notation, the fundamental frequency is used to name the notes. For instance, in the Western music system, the note A4 is defined by a fundamental frequency of 440 Hz.
This means the A4 note produces a sound wave with 440 cycles per second. As you move up or down the musical scale, the fundamental frequencies of the notes increase or decrease, respectively.
Fundamental frequencies are critical in music because they form the basis for melodic and harmonic structures.
Melodies are composed of sequences of different fundamental frequencies, while harmonies are constructed based on the relationships between the fundamental frequencies of different notes played simultaneously.
Overtones (Harmonics)
Overtones, also known as harmonics or partials, are higher-frequency components that accompany the fundamental frequency of a sound. The physical properties of the sound-producing object or instrument generate them.
When you play a musical note on an instrument, the sound is not just a pure sine wave at the fundamental frequency. Instead, it contains additional frequencies integer multiples of the fundamental frequency. These higher frequencies are called overtones or harmonics.
The presence and strength of overtones vary from one instrument to another, giving each instrument its characteristic timbre or tone colour. For example, the overtones in a piano note differ from those in a violin or flute note, even when playing the same fundamental frequency.
In music, the combination of the fundamental frequency and overtones creates a complex waveform that is unique to each instrument or sound source. This complexity in the waveform is what gives instruments their distinguishable sound qualities.
Overtones play a crucial role in shaping musical sounds’ richness, brightness, and complexity. They add texture and depth to the sound, making it more interesting and pleasing to the ear.
Manipulating the presence and strength of overtones is a key aspect of sound synthesis, sound design, and audio engineering.
Techniques such as filtering, equalization, and modulation can enhance or modify the overtone structure of sounds, allowing for creative exploration and artistic expression in music production.
| Fundamentals | Overtones |
| Perceived pitch/frequency of the sound | Additional frequencies/notes that may not be easily perceivable but contributes to the timbre of the sound |
| Common link between two instruments/voices playing the same note | What differentiates any two voices/instruments playing the same note |
| Usually the lowest note/frequency of the sound | Usually a derivative/multiple of the fundamental |
| Only one fundamental exists for sound | Multiple overtones exist for a sound |
In summary; the fundamental frequency defines the pitch of a musical note. In contrast, overtones contribute to the timbral quality of the sound. Overtones add complexity and richness to a musical tone, while the fundamental frequency provides the primary pitch information.
Together, the fundamentals and overtones create the unique sound signature of each musical instrument and contribute to the overall texture and color of the music.
Understanding and controlling these elements are essential in music composition, performance, and audio engineering to achieve specific sonic outcomes and artistic expressions.
What is the Relationship Between a Fundamental Note and its Overtones?
The relationship between a fundamental note and its overtones is that overtones are higher-frequency components that accompany the fundamental frequency.
Harmonics (a specific type of Overtones) are integer multiples of the fundamental frequency, and their presence and strength give each instrument its unique timbre or tone colour.
Now, let’s explore that relationship mathematically, which can be expressed mathematically using the formula: Frequency of the nth overtone (Fn) = n * Fundamental frequency (f0) where:
- Fn is the frequency of the nth overtone,
- n is a positive integer greater than or equal to 1, representing the harmonic number, and
- f0 is the fundamental frequency.
For example, if the fundamental frequency (f0) is 440 Hz (A4), the first few overtones are:
- First overtone (second harmonic): 2 * 440 Hz = 880 Hz
- Second overtone (third harmonic): 3 * 440 Hz = 1320 Hz
- Third overtone (fourth harmonic): 4 * 440 Hz = 1760 Hz
- And so on.
In terms of audio engineering, the frequency with the highest amplitude, loudness, or intensity is the fundamental frequency. Overtones are harmonics are all the other frequencies and are softer than fundamentals or have lesser amplitude and intensity.
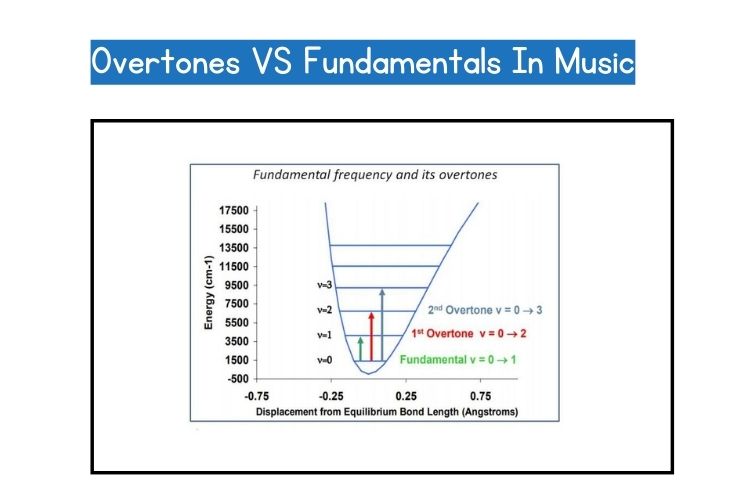
Visually, the relationship between a fundamental note and its overtones can be represented using a waveform or a spectrum graph. In a waveform graph, the fundamental note is depicted as the main, largest waveform representing the fundamental frequency.
Overtones are shown as smaller waves above the fundamental frequency, with the second overtone having double the frequency, the third overtone having triple the frequency, and so on.
In a spectrum graph, the fundamental frequency is represented as a peak or spike on the graph, and the overtones are depicted as additional peaks at integer multiples of the fundamental frequency.
The higher the harmonic number, the higher the frequency of the corresponding overtone.
Conclusion
The relationship between a fundamental note and its overtones is that overtones are additional lower amplitude components that accompany the fundamental frequency and determine the sonic qualities of the sound without altering its primary pitch or note.
In fact, using overtones creatively with distortion and saturation can lead to exciting and unique sonic textures in music production. Using these harmonic enhancers or processors, you can introduce interesting characteristics to your sound.
In fact, in music production and mixing-mastering, these tools are extensively used to alter the overtone or harmonic structure of the sound.
I hope the article helps you understand the basic difference between fundamentals and overtones. Thank you for reading.